The third in a series of blogs covering common mistakes in Database and Application designs for financial calculations.

Order of Operations and Storing Aggregate Results:

When working with float data types, order of operations will affect the ending value.

Consider 3:

Python3:

justin@Debian10:~$ python3

Python 3.7.3 (default, Jul 25 2020, 13:03:44) 

>>> (1234.567 * 3.333333) + (1.234567 * 3.333333)

4119.338,144,732,812

>>> (1234.567 + 1.234567 ) * 3.333333

4119.338,144,732,811

As can be seen with the example, order of operations affects the result even though associative and communicative rules state it should not. The degree to which it affects the result depends on if it is a 32 or 64 bit floating type.

Many are going to state that it's only 1 digit of error, however this is happening in one operation and should not happen. This error is amplified when stacking results on results.

A real world example of this problem is with cost-based accounting, recalculating the cost of items using a Weighted Average formula to calculate the average cost.

Formula:

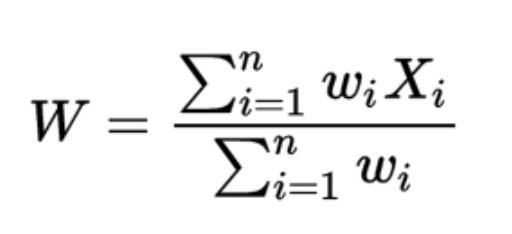
Where:

• W = weighted average
• n = number of terms to be averaged
• wi = weights applied to x values
• Xi = data values to be averaged

Or more simply expressed below to calculate system/application wide unit cost:

SystemItem UnitCost = ((QtyOnhand/(QtyOnHand + NewQty)) * CurrentCost) + ((NewQty/(QtyOnHand + NewQty)) * NewCost)

The above formula will return the new cost of an item on a per unit of measure basis. The application must independently track the cost and the quantity on hand for each item. To calculate the total value of inventory is done like so:

QtyOnHand * SystemItemUnitCost = SystemItemTotalCost

However, many implementations calculate the Weighted Cost using an aggregate value of the Total Cost. This makes calculating the new weighted average easier:

SystemItemTotalCost = CurrentItemTotalCost + (NewItemTotalCost)

This approach is simpler and appears to work, but errors start creeping in as the “per unit of measure cost” is calculated at every transaction, which updates the system total cost and quantity on hand.

PerUnitCost = CurrentItemTotalCost/QtyOnHand

SystemItemTotalCost = CurrentItemTotalCost +/- (QtyOfTransaction*PerUnitCost)

QtyOnHand = QtyOnHand +/- QtyOfTransaction

The bulk of the error comes from recalculating the PerUnitCost at every transaction, adding rounding and floating point errors to the new results.

Consider 4:

SELECT '1: Calculate new cost', round(((139.00/(139.00+75.00) * 1.25)) + ((75.00/(139.00+75.00))*1.35),4), round((((139.00 *1.25) +(75.00*1.35))), 4)

UNION

SELECT '2: do a transactions subtract 5.333, value moved', round( 1.2850 * 5.333, 4), round(275.00/(75.00+139.00) * 5.333, 4) 

UNION

SELECT '3: do a transactions subtract 37.482', value moved, round( 1.2850 * 37.482, 4), round((268.1468/208.667) * 37.482, 4) 

UNION 

SELECT '4: do a transactions subtract 68.57, value moved', round( 1.2850 * 68.57, 4), round((219.9807/171.185) *68.57, 4) 

UNION

SELECT '5: Total inventory value',  round(1.2850 * 102.615,4),  130.8247

UNION

SELECT '6: Current per unit value',  1.2850 ,  round(130.8247/102.615,4) 

ORDER BY 1

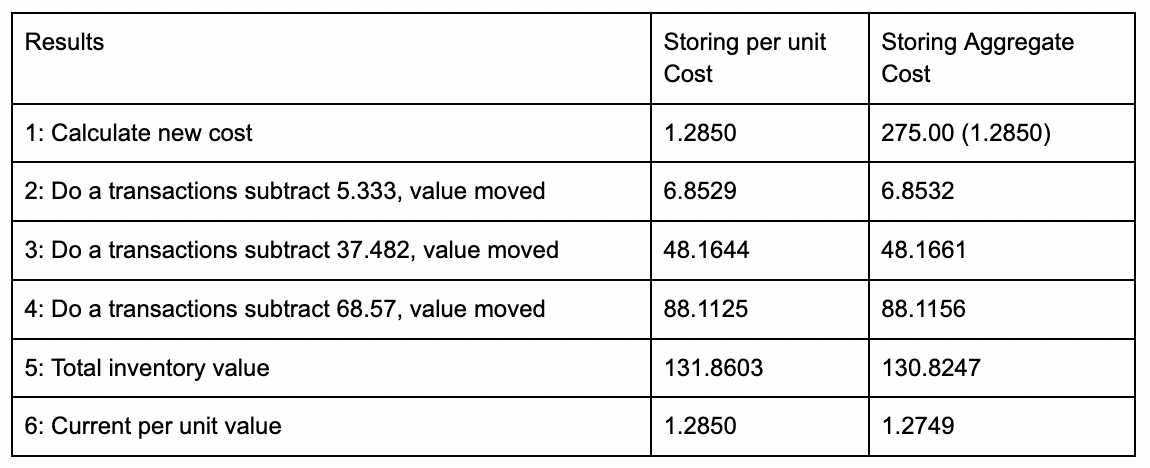
We see here how the order of operations and storing of an aggregate value distorts calculations rather quickly. With only 3 transactions, the total inventory value was distorted by 0.04 units.

The above calculations were done with PostgreSQL numeric type, not a floating point type. Using float type would make the deviation worse. If we threw in units of measurement conversions, the deviation would grow. See Consider 2 for effects of unit of measure conversion.

The solution:

If the application uses aggregates in critical calculations, the quickest solution is to increase precision of the stored values and in all calculations. This delays the stack up error from wreaking havoc. The error can not be completely removed by only increasing the precision. The best approach is to keep the stored values in the lowest common value, and avoid storing or using aggregated, sum, or grand totals that are used in later calculations. For example do not store the total inventory value (Qty * UnitCost); store the quantity on hand and the unit cost in separate columns. Best to avoid using mix precision, rounding, or simplifying formulas with calculated aggregated values. Don’t cheat or shortcut the math formulas to save processing time. CPU time is cheap today; this is not the 1970’s.

Closing thoughts:

Watch the structure of formulas and order of operations. It's easy to add errors to a result that will go unnoticed for thousands of operations. Always investigate what will happen if a formula is called thousands or millions of times.

Is the result correct?

How much error can be tolerated?